Proposal Bot/Spring/2020
Bezier Curves
Author: Tyler Galgas
Introduction
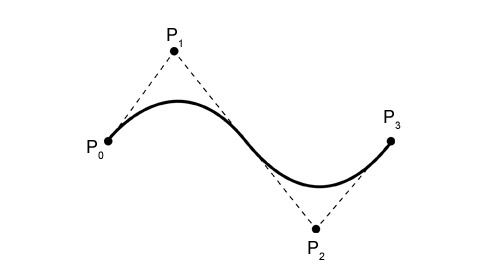
Bezier curve is the name given to the parametric curve controlled by a set of points. Used often in computer graphics, animations and fonts, Quadratic Bezier curves are composited together to form a sequence of curves.
Properties
As defined by Pierre Bezier
- The Bezier curve is always constrained to a polygon called a convex hull determined by it’s control points.
- The shape of the curve generally follows the shape of the polygon; the first and last points of the curve fall on the first and last points of the polygon.
- The degree of the polynomial is the number of control points minus one.
- The order of the polynomial is equal to the number of control points.
- Bezier curves exhibit the variation diminishing property; the curves are smoother than the polygon defined by the control points.
Parametric Equation of a Bezier Curve
Where,
- p(t) = any point falling on the Bezier curve
- Bi= ith control point of the Bezier curve
- n= degree of curve
- Jn,i(t)= blending function = C(n,i)ti(1-t)n-i where C(n,i) =n!/i!(n-i)!
Composite Bezier Curves
By using a series of Bezier control cages, tangent points can be stitched together and formed into a composite that resembles a curved drawing. This can be used for modeling anything that needs to be displayed or drawn in a curved/cursive fashion.
Conclusion
Through stitching together tangent vector points with their contained Bezier curve, letters could be fashioned in cursive on Proposal Bot.