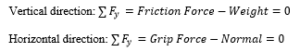Fall 2016 Prosthetic Hand: Force and Torque Calculations

Fall 2016 Prosthetic Hand: Force and Torque Calculation

Mission, Systems, and Test Engineer – Mia Lai

Table of Contents

Minimum Grip Force

Grip force is the force that the fingers apply on the object to hold the object against gravity. In our project, the prosthetic hand will pick up three difference food items: a 21-oz cup of soft drink, a 7-oz (198-g) burger, and 2-gram to 20-gram bundle of fries. Among these three food items, the 21-oz cup of soft drink is the heaviest item that the hand must pick up. Therefore, the design of the hand system must provide a sufficient grip force to hold the cup of soft drink.

Figure 1 – Free Body Diagram

Assumption:

The acceleration of the arm is zero. Acceleration will add more weight to the cup if the arm moves up quickly [2]. However, our prosthetic system will move at a slow speed when lifting the cup so that acceleration will be neglected in the calculation.

As shown in the free body diagram, in order to maintain the cup from slipping out of the hand, the static friction force must be equal to the weight of the cup.

Friction Force = µ*N where µ is the coefficient of static friction and N is normal force, which is equal in magnitude and opposite in direction to the grip force provided by the prosthetic hand system.

Weight of cup = m*g where m is mass of the cup and g is Newton’s constant

Solving for forces acting on the cup vertically and horizontally, we have: µ N = m*g

Mass of 20-oz (621-ml) cup of soft drink:

Mass = volume of cup * density = 621 ml * 1.1 g/ml = 683 grams
Note: Density of regular coca-cola = 1.1 g/ml [6]

Static friction coefficient between the prosthetic finger material and the cup material: µ = 0.5 (We assumed that the hand and the cup is made of plastic) [1]

Minimum Required Grip Force = m*g/ µ = 0.683 * 9.8/0.5 =13.4 N

Minimum Gripper Torque

For gripping torque calculation, we used gripper torque formula as a mathematic model to calculate minimum required torque for our prosthetic hand system because the grasping mechanism of the prosthetic hand is similar to grasping mechanism of a gripper.

Gripper torque: T = Required Grip Force * Jaw length [3]

Jaw length (moment arm length) is measured from the face of the gripper to the center mass of the object [3]. In our design project the moment arm length is radius of a medium cup, which is equal to 37.5 mm (We assumed that the hand will pick up the cup at the top part of a cone-shaped cup) [5].

Required Grip Force is 13.4 Newtons, which is dictated in the grip force requirement as a level 2 requirement.

Gripper torque = 13.4N * 0.0375 = 0.5025 Nm

In our design, there is a rubber band at the back of each finger. The rubber band acts as a spring to pull the finger back to its original position. In order to provide a 13.4-N grip force output, the system must provide input grip force that is equal to the sum of output grip force and rubber band force.

Input grip force = Output required grip force (13.4 N) + Rubber band force (0.5 to 5 N)

Figure 2 – Rubber Band on 3D Printed Finger

The rubber band force is around 0.5-5 Newtons [4]. According to Hooke’s Law, pulling force f rubber band is proportional to the stretch of the rubber band, which depends on flexion level of the finger. Instead calculating pulling force of rubber band we will use safety factor in our calculation. The minimum required torque is the gripper torque multiplied by a safety factor of 1.4.

Minimum grip torque required for the whole system = Gripper torque * Safety factor

T_system = 0.5025 *1.4 = 0.7035 Nm

Thus, minimum torque required for each motor controlling the gripping motion of each finger

T_motor = System Torque / number of fingers = 0.7035/ 5 = 0.14 Nm

Moment of Intertia and Rotational Torque

For this design the hand will have ability to rotate at the wrist base. For the hand to rotate from resting position, torque is required to produce a desired angular acceleration. The torques acting at a pivot point is equal to the moment of inertia multiplied by the angular acceleration: T = I * α. We assume that the hand will accelerate from 0 to 280 degree/second in 1 second. The estimated speed of hand is obtained from suggested speed for prosthetic device [7].

Moment of inertia is the object’s tendency to resist the angular acceleration. It depends on mass and shape of the object. In our design, because the hand does not have any regular shape, we will use the formula of the moment of inertia for a solid cylinder to calculate to rotational inertia of the hand:

Where M is the total mass of the rotating objects

M = allocation mass of hand + mass of heaviest food item = 615+ 683 = 1298 gram

(Note: We calculated the worst case scenario that the hand rotates while holding a cup)

Angular acceleration α = 280⁰/s² = 4.89 radian/s²

Thus, the calculated rotation torque needed to rotate a cylinder-shape hand for a desired angular acceleration of 280⁰/s² about a rotational axis is:

T = I * α * safety factor = 0.0013 * 4.89 *1.5 = 0.01 Nm

Since the moment of inertia varies with the shape of the hand, the safety factor should be enhanced respectively for different shapes of the hand. We choose safety factor of 1.5 to account for the difference in shape of the hand. Therefore, the stepper motor must be capable of providing torque of 0.01 Nm to rotate the hand at a desired acceleration of 280⁰/s²