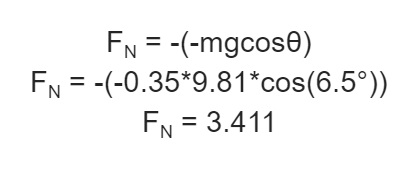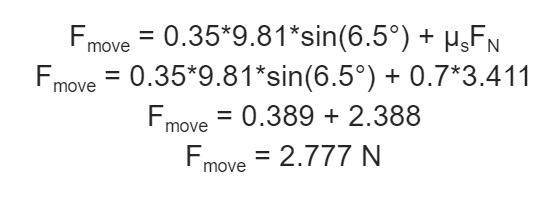Goliath Fall 2016
Torque Calculation for Going Up a Ramp
By: Diana Nguyen (Missions, Systems, and Test Engineer)
Approved by Kristen Oduca (Project Manager)
Introuction
Requirement: To drive the Goliath up the 6 degree incline, the motor shall provide a minimum torque of 0.0249 Nm.
For the Save the Human Game, there will be two ramps in the course of the game. Both ramps will have a 6.5° incline, plateaus and then decline 6.5°. Goliath will need to be able follow the biped up the ramp and across it.
Calculations
Goliath needs to be able to go up a ramp with an incline of 6.5°. The mass of Goliath is 350 g or 0.35 kg and the static coefficient of friction for rubber and cardboard is between 0.5-0.8 [1]. We need to be able to produce enough force to be able to move the Goliath up the ramp which would be Fmove.
From Figure 1 we can see that FN is the opposite force of -mgcosθ. Therefore we can assume FN = -(-mgcosθ).
Since we now have FN and we know µs ,which is the the static friction. We can complete our calculation of Fmove.
Using this we can now calculate the amount of torque the motors need to produce. Torque can be calculated from Torque = (Radius of shaft) * Fmove.
Figure 5 shows the diagram of the forces.
Conclusion
Base off these calculations we can conclude that based off our current model Goliath we need a motor with a minimum torque of 0.0528 Nm. After our motor test we can see if the motors we purchased be able to produce this minimum amount required to go up the ramp.