For this mission we will will need to know a couple things before we can clear the loop. One of the things that we will need to know is the the velocity. In order for this to work we need to make sure that sure that the centripetal force is at least equal to the cars weight. From this we get centripetal force and weight of car
by setting there two equations equal to each other we get
by further simplifying this equation we can see that the mass will cancel out and out new equation will be
as we can clearly see the radius we will be clearing will be dependent on the velocity alone. Once we know the top speed of our car we will be able to easily calculate the loop it can clear.
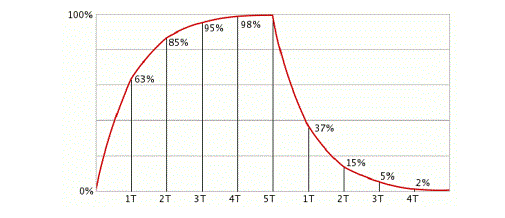
In order to get best boost we can get to clear the loop we must make sure that our capacitor has enough time to get fully charged. Our capacitor voltage charge is dependent on the equation when t=RC we have gone through one time constant that would only make up 63% of the full charge. 63% of the full voltage charge for our capacitor will be at 7.56 v. So when probing the capacitor circuit we will be looking for the time it take to reach this voltage value in order to get out time constant. It will take about 4 to 5 time constants to fully charge our capacitor. We will also need to calculate the time constant for discharging the capacitor since the resistance for charging and discharging the capacitor will be different. We will be looking for the voltage at 37% of the fully charge when discharging. Time it take to go from 12 v to 4.44 v.
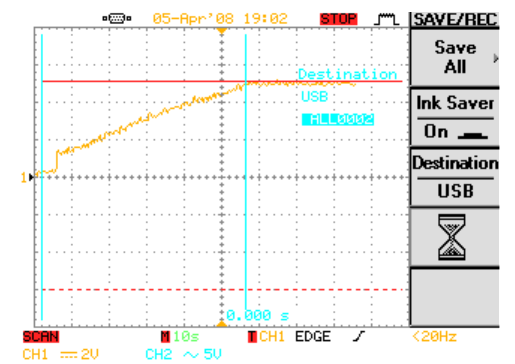
In this graph we have the capacitor charging up to 12 v. Using the cursors we measure the time it takes for the capacitor to be fully charged at 50 seconds.
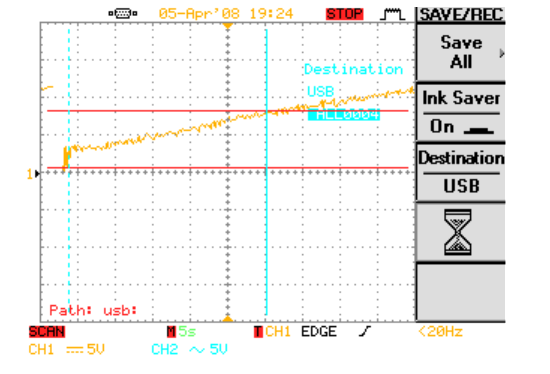
In this graph we are measuring the time constant for the circuit charging the capacitor. We do this by measuring how long it takes to get to 63% of full charge. In this case 63% charge will be at 7.56 v the closest we can get to this value was 7.6 v so the time it took to get to this values was 26.4 seconds.
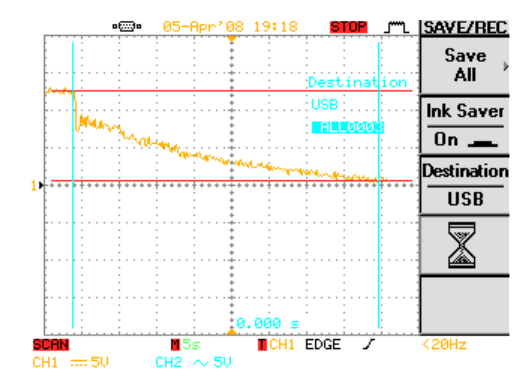
In this graph we have our capacitor discharging. This is a rough estimate of how long it will take for our capacitor to discharge. Since we don’t have the motors that will be used for modwheels yet we decided to discharge onto a spare motor. The discharge time was 40 seconds for this motor.
plans to measure the time for the capacitor to charge below 5 V and the discharge time constant with a two motor load. looking into slip differential a encoder will be needed to to find out the car speed and measure the difference in tire rotation.