Assembly Robot PreLab 1 – An Amazing Programming Problem

View Exclusively

Table of Contents

The Original Problem

The problem we will be trying to solve for the semester was originally taken from a puzzle book. Here is the problem as defined by the puzzle book.

“In the forest, you will find beehives and more importantly honeycombs. Along the path are bees. The number of bees at any given location is indicated by a number. There are a few ways your bear can travel to the forest. Your aim is to teach your bear how to make his way to the forest while encountering as few bees as possible”

Take a few minutes and see if you can solve the puzzle.

Figure 1: The Maze

For this semester, we will be using an updated maze that allows for a little more customization based on your tastes. If you took a look at the playing cards within your maze kit, you will find several different playing cards that you can print out and will be placing throughout the maze. There is a core set of rules and conditions that we will follow to keep the labs manageable but you will be able to have some fun with the theme of your personal mazes.

Figure 2. Latest Maze

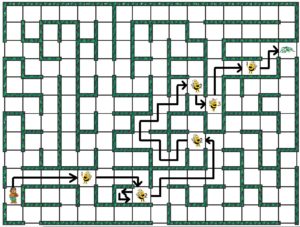
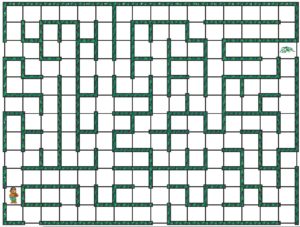
To provide a basic example to work with, we will be using a bear to represent the robot and it will be passing by / collecting a certain number of objects (bees) as shown in figure 3. The focus of this prelab is to guide you through the steps for solving the problem of navigating through the maze with the selected path. While it may seem unrelated to writing the actual code, these are core concepts that you will need to understand in order to succeed in the class.

Figure 3 – Example Path

Draw A Flowchart

The first step to take when approaching any programming problem is to create a high level representation of what the code needs to do in the form of a flowchart. While most of this work will not be directly translated into code, it is an essential step to identify potential ways to structure the program and possibly catch any mistakes before spending time to implement it. Some of you may not know where to start for such an open ended problem like writing a program to help the bear navigate the path shown and the best way to develop your own method is through experience. Now let’s see if you can translate your path through the maze into a flowchart. Everything provided below is to be used as a reference on how to break down the problem into manageable parts. Keep in mind, you are not limited to only what is listed.

  1. Assume the Bear is initially facing north at the entrance into the maze. The Bear has a way to keep track of the number of objects it has passed which is a notepad. The length of each step is exactly one square.
  2. There are certain things that the bear can do or check in the attempt to exit the maze. The bear could take a step into the next room, check to see what type of room is encountered, or decide on which way to go next. The entire list of instructions that the bear can take are listed below. Compare it with your own list of instructions that you thought of to see how close you were.

Actuators and corresponding unconditional instructions

  1. Take a step.
  2. Turn left
  3. Turn right
  4. Turn around
  5. Count and record the number of bees in the current room.

Sensors and corresponding conditional instructions

  1. Did you hit a wall?
  2. Can your left paw touch a wall?
  3. Can your right paw touch a wall?
  4. Are you out of the maze?
  5. Do you see any bees?
  6. Are you thinking of a number {not equal, less than, greater than or equal} to 0?
  7. Is the number the Bear is considering {not equal, less than, greater than or equal} to some constant?

Memory operations

The bear can remember 8-bit unsigned and 1-bit (binary) numbers. The bear records a number in his notepad. He can only save one number per page. You may assign a descriptive name to a page (ex. bees), simply use the page number (page1), or think of it as a variable (X). In the following example X = 0.

C++ Equivalent Instructions

  1. Erase page X.                                page0 = 0;
  2. Increment the number on a page. page0++;

Nodes

  1. Start
  2. Stop

Tips and Tricks

  • You may not need all the instructions provided.
  • Although not required, you can use subroutines.

Take a few minutes to see if you can sketch-out your flowchart. If you don’t know where to start; don’t worry, in the next few sections, I will step you through how to write your own flowchart.

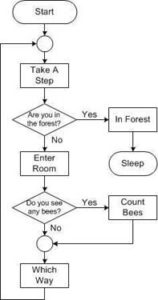
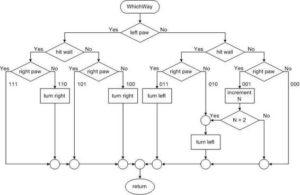
  1. The path through the maze can be modeled as follows. Figure 4 provides an overview of everything the bear will be doing to get out of the maze. Each block will be expanded on in future labs to describe exactly what our assembly program will be doing. The order that certain actions are done could be swapped around in your solution but this is how we will be implementing it. For example, this prelab will focus on defining the “Which Way” block, which determines the direction the bear should face while going through the maze.

Figure 4: Top Level Flowchart of maze problem

Creating the WhichWay Flowchart

First, we need to clarify what the Which Way block will be doing. From Figure 4, we know that the bear has just entered a room in the maze and now needs to determine which direction to go. The bear will be taking another step after the Which Way block, so we only need to make sure that the bear is in the correct orientation. There are two ways the bear can decide which way to turn when entering a room. You can count how many rooms the bear has passed or identify what type of room the bear is in. We will be doing the latter for our lab. Based on this information, these are the only instructions needed for this flowchart.

  1. Turn left
  2. Turn right
  3. Turn around
  4. Did you hit a wall?
  5. Can your left paw touch a wall?
  6. Can your right paw touch a wall?
  7. Increment the number on a page
  8. Is the number on page N of the notepad {not equal, less than, greater than or equal} to some constant?

With that in mind, we need to define a way to identify the rooms the bear enters.

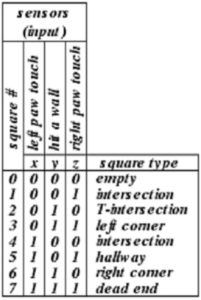
Square Naming Convention

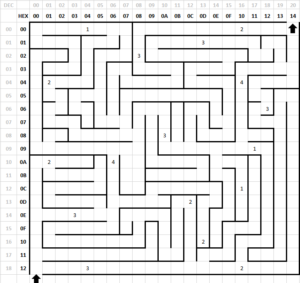
Here is a standardized naming convention to help you define the decision points in any maze. In order to provide a design example, the following maze identifies the squares (i.e., intersections) where the bear needs to make a decision for the shortest path solution.

Figure 5: Labeled Example Path

Squares are numbered by concatenating the binary values (yes = 1, no = 0) for the answers to the following three questions (sensor inputs).

Can your left paw touch a wall? – Did you hit a wall? – Can your right paw touch a wall?

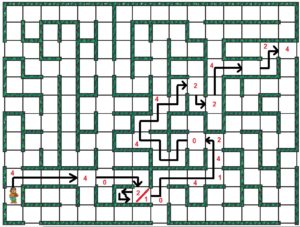
The answers to these three questions provide all the information that our bear can know about any given square. Let’s look at a few examples to see how this works. After taking the first step, the bear can touch a wall with his left paw (1), has not hit a wall (0), and cannot touch a wall with its right paw (0). For our convention, this would correspond to input condition 4 = 1002. As seen in the illustration I have therefore numbered this square 4. Assuming the bear turns right; after taking another step the bear finds himself in a hallway where his left and right paws touch a wall and he does not hit a wall. This corresponds to square 5 (1012). Although you could write a 5 in this square, for the sake of brevity, I left it blank (your bear walks down a lot of hallways). Notice that the numbers are based on the direction the bear is facing and not a universal reference point, like facing north. This corresponds to the fact that within the maze our bear has no idea where north, or any direction for that matter, is (our bear forgot his compass). So, let’s continue to the next intersection. Here the bear’s left paw is touching a wall (1), he does not hit a wall (0), and his right paw cannot touch a wall (0). We therefore would write another 4 (1002) in this square. Continuing in this fashion, all intersections are identified for our minimum solution. When you have squares that you pass through twice, please indicate the order by using a / to separate the numbers. For example, there is one square in the example path that has 2/1. This means that the square is considered type 2 when the bear enters it for the first time when it comes down and it is considered a type 1 when returning from the dead end.

Using this notation, the only squares that need to be labeled are the intersections (0, 1, 2, and 4). All other squares can be left blank as indicated in figure 5.

Example Path Solution

Using the square naming convention and the example path through the maze presented in the last section, let’s design a solution for the actions the bear needs to take.

Build a Truth Table

Table 1: Shortest Path Solution

For your minimum solution, your bear should encounter all square types. Once again we did not include in our illustration situations where the bear has no choice (3 = left corner, 5 = hallway, 6 = right corner, 7 = dead end).

Draw your Flowchart – Solution for a Fully “Deterministic” Maze

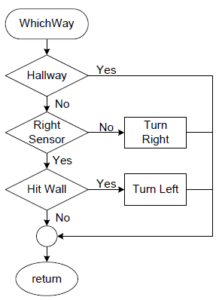
A fully deterministic maze is one where for any given intersection the bear will always (it is predetermined) take the same action. For example, whenever the bear encounters intersection 4 he will always turn right. For a non-deterministic maze, he may turn right one time and turn left another. The complexity of the sequence of actions will depend on what your path looks like. If we to consider one of the simpler deterministic algorithms possible for the WhichWay block, it could look like what is shown in Figure 6. There is no ambiguity about what should happen if this is the 5th hallway the bear has encountered as everything is clearly laid out. However, it is very unlikely that the path that you create later in the lab can be handled with a deterministic solution.

Figure 6: Deterministic Path Solution

Once you have your flowchart, implementation in the C programming language or Assembly is fairly straightforward.

Prelab 1 Assignment

At this point, we are ready to discuss how you will be defining your unique path through the maze. Starting with the blank maze, one of the many entrances has to be chosen for your start point and the exit has to be chosen in the opposite quadrant. For example, if an entrance is chosen in the bottom left like in figure 7, then the exit used has to be within the top right. They are indicated using the bear playing card and green waves playing card.

Figure 7: Selecting your entrance and exit

Because the maze is a 16×12 grid, you can divide it into four quadrants and figure out which one is opposite to the entrance that you choose. Once you have defined those two spots, we can move onto the target square.

Find Your Target Square

There will be one location that the bear has to pass through on its path. This target square is determined from your student ID number. Write down the last four digits of your student ID as two 2-digit decimal numbers. These digits will provide the coordinates (row and column) of your target square. For example, if the last four digits of your student ID were 7386, your two 2-digit numbers would be 73 and 86. Divide using long division on each number and write the remainder down. Specifically, the row will be divided by 12 and the column will be divided by 16. Those remainders are now your row and column numbers. In our example, 12 divides into 73 six times with a remainder of 1 and 16 divides into 86 five times with a remainder of 6. Next convert the remainders into a hexadecimal (base 16) number. For our example, 1 = 0x01 (where the prefix 0x signifies a number in hexadecimal) and 6 = 0x06. Your target square would therefore be in row 0x01 and column 0x06.

How to Find Your Path

In addition to the target square, there are several conditions that need to be met for your path to be considered valid. Design a path through the maze such that:

  1. The bear goes through the target square.
  2. The bear must get lost at least once. Specifically, he must at some point turn-around. This is typically, but does not need to be, at a dead end.
  3. The bear encounters at least 10 bees but does not exceed 15 (inclusive). Placement of the bees is left up to you with the bee playing cards. Try to spread them randomly throughout the maze. You are allowed to only use the 1, 2, and 3 bee cards. If you would like to use the higher number cards, please discuss it with your lab instructor.
  4. Finally, the maze must be non-deterministic. This means that at some intersection along the path the bear will need to take a different action. For example, the first time he encounters a T-intersection he turns left and the second time he turns right. The good news is that, if your path meets the first three criteria, the odds are extremely high that it will be nondeterministic.

Figure 8: Example bee card

Let’s look at how you can develop a flowchart for your unique path.

Design Methodology for a “Non-deterministic” Maze

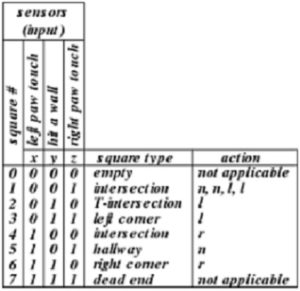
As previously mentioned, most maze solutions are non-deterministic. The phrase “not fully deterministic” means, while one set of input conditions in one part of the maze will determine one action (go straight), in another part of the maze the exact same conditions will require a different action (turn right). By looking at your truth-table you can recognize a “non-deterministic” path as having two or more 1’s in the same row. A quick inspection of the truth table generated from the deterministic path solution(Figure 6) reveals that the bear follows a fully deterministic path. Specifically, for any given intersection the bear will always take the same action. For example, if the bear’s left paw is touching a wall (1), he does not hit a wall (0), and his right paw is not touching a wall (0), then the bear will always turn right.

Sensors
Square # Left Paw Hit Wall Right Paw Square Type Action
0 0 0 0 Empty / 4 way Intersection Turn Right
1 0 0 1 Intersection Forward
2 0 1 0 T-intersection Turn Right
3 0 1 1 Left Corner Turn Left
4 1 0 0 Intersection Turn Right
5 1 0 1 Hallway Forward
6 1 1 0 Right Corner Turn Right
7 1 1 1 Dead End N/A

Table 2: Truth table of Deterministic Path

Take some time to see if you come to the same list of actions as shown in table 2. Keep in mind that the action for square type 7 is N/A or not applicable because there is no possible action for it based on the deterministic path algorithm. You are only able to use N/A in your truth table if the bear will not encounter it on the path and therefore does not need to consider an action for it. For those of you that spent the time to test what the algorithm will do for the example path we have, I know that the bear will be stuck in a dead end but that is the purpose of these examples (to get you to start thinking about it). While this seems pretty simple, your unique path is non-deterministic and will be a bit harder. Let’s begin by looking at this example and use it to build the truth table for your path.

Table 3: Sensor Input Combinations and Actions for Non-deterministic Path Example

The good news is that with the exception of square number 1 all other actions are deterministic. The bad news is that only when we encounter room 1 after the second time do we start turning left. Please note that each action for square type 1 is listed because we need to see when the actions in the sequence change. You can infer from the table that the path will have four encounters with square type 1 and there is a specific action for each time you pass that square type. If those actions are not followed, the bear will go down a different path and not your unique path. This does not mean that the other square types are only encountered once. They have been condensed into one action because it turned out to be deterministic for that square type. You should still keep track of the sequence of actions for each square type as you are analyzing it and reduce it down to one if it satisfies the condition for being deterministic. To solve this more difficult problem of handling square type 1, we will create a binary tree that allows us to resolve all 8 squares, allowing us to then take any action needed. This binary tree can now be easily translated into C++ or Assembly.

Figure 9: Flowchart Showing Binary Tree Solution to Non-deterministic Path Example

This allows us to break up what the WhichWay subroutine will need to do for this specific path into implementable blocks of code.

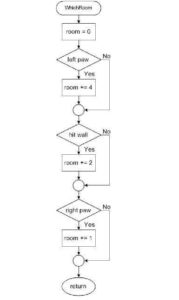
EXTRA – A Modular Solution

For those of you with some previous programming experience, we can approach this problem with a more elegant solution. FOR THE PRELAB, you do not need to do it this way. A more modular solution separates the identification of the square (referred to as a room) from the action to be taken. Identification of the room is placed into a C++ or Assembly subroutine which returns the room number. The calling program must then determine the action to be taken based on the room number returned. The flowchart for the room subroutine is provided here and once again easily implemented in C++ using if or switch conditional instructions as discussed in the next lab.

Figure 10: Flowchart of Which Room Subroutine

Disclaimer – The discussion about the modular solution is to introduce you to other possible methods for approaching this problem. It is representative of how programming can be done in a variety of ways. You do not need to make a flowchart similar to this one.

Step-by-Step Instructions

After all of that background information, here are the step-by-step instructions for the prelab 1 assignment.

Begin by making a copy (electronic or paper) of the maze and drawing your bear’s path through the maze.  When you are happy with your new path, follow the methodology previously discussed to build your truth table. Verify that your path meets the design criteria (passes through target square while encountering the minimum number of bees and getting lost once). Remember, your target square may not be along the original solution path.

It is now time to teach your bear how to navigate the new path by writing a flow chart. To accomplish your goal, you will need to apply everything you have learned so far plus add a few Notepad operations. The notepad pages (i.e., variables) are used to determine which path your bear should take when he enters an intersection in which more than one action is possible. For, example the first time he enters intersection 1 you may want the bear to go straight, while the second time he encounters intersection 1 you want him to turn left. To resolve this conflict you would record in your notepad how many times intersections 1 had been encountered and then check your notepad before taking any action.

In addition to previously stated conditions, your solution must also meet the following negative criteria.

  1. Your solution may not use a variable (notepad) to simply count how many steps the bear has taken in order to make a decision.
  2. Your solution should use a variable(s) and not the number of bees encountered to help it make a decision.

Deliverables for Prelab 1

Turn in the following material on the following pages (i.e., no more, no less). All work must be typed or neatly done in ink.

Title Page (Page 0)

The title page (Page 0) includes your picture (one that will allow me to match a name with a face), the lab number, your name, today’s date, and the day your lab meets.

Page 1

At the top of the page provide the last four digits of your student ID and describe how you calculated your target square. Include in your discussion how the resulting path met the design requirements defined in the pre-lab. For example how many paths did you consider before choosing your final path – how close did you come to 15.

Page 2

Next, using your favorite illustration (Visio, Illustrator, or Photoshop) program or the drawing tools included with your favorite Office program (PowerPoint, Excel, and Word), mark your target square with an X and illustrate your bear’s path through the maze just like Figure 3. Include a second illustration that marks all of the intersections that the bear will need to make a decision at. Make sure to number your intersections (but not corners or hallways) as illustrated in Figure 5. You may remove / white out the bees that were placed throughout the maze in order to clearly show the numbers.

The last thing to include is the truth table for your path as explained above with a format similar to Table 2. If you do not have access to any of those programs, there is a free online website called www.draw.io that works just fine. Please make sure everything is legible. You may use more than one page for this if there is not enough room.

Page 3

Again using your favorite drawing program, draw the flowchart for your path. It should be based on the truth table from Page 2 and look similar to Figure 9.

Your flowchart should resemble the one included with the lab and only use the provided instructions. Artwork of the sample flowchart can be found here.

Page 4

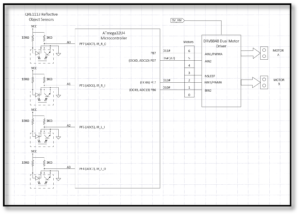
The goal of Lab 1 is to use two of the four input object sensors to control the motors in such a way that the robot will follow a black line. We will spend some time discussing how each part operates and start with a couple of questions to see how much you already know. Provided below is a diagram of how the IR sensors and motors are connected to the microcontroller.

Figure 11: Object Sensor to Motor Driver

Question 1: How many connections need to be made based on the the objective described? For example, will it be 1 to 1, 1 to 4, etc?

Question 2: Based on Figure 11, how should the input and output signals be connected so that the robot can follow a line. Hint: Read Lab 1. For example, should AIN1 be connected to IR_R_I (the inner right IR sensor) or the other way around?

All labs should represent your own work – DO NOT COPY.

Checklist

  1. Your pre-lab report includes a title page (Page 0) with your picture (one that will allow me to match a name with a face). Title information includes lab number, your name, today’s date, and the day your lab meets (Monday or Tuesday)
  2. Pages are in the order specified (see Deliverable)
  3. You do not have any extra pages
  4. You describe how you arrived at your path.
  5. Maze is not copied from another student (zero points)
  6. Path is computer drawn.
  7. Maze Path meets specified requirements.
  8. Intersections are not drawn by hand and appear as shown in the example.
  9. Intersection are numbered
  10. Intersections are numbered correctly
  11. Truth table
  12. Truth table is on the same page as the maze
  13. Truth table is typed
  14. Truth table matches the maze
  15. Flowchart
  16. Flowchart matches your truth table
  17. Flowchart is correct
  18. Question(s) are answered with all work shown.