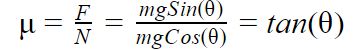E-Racer/Spring /2019
Coefficient of Friction
Author: Jeremy Anderson
Verification: Jennie Lim
Table of Contents
Introduction
The E-racer’s functionality requires it to remain attached to a whiteboard. In order for the robot to overcome the force of gravity and keep from falling, an equal and opposite force must act on the robot. This force is the frictional force, which is created by the contact of the robot’s treads with the whiteboard in conjunction with a force that squeezes the two surfaces together. The ratio of the frictional force to this squeezing force is called the coefficient of friction. Knowing the coefficient of friction will allow the magnetic force to be defined as a function of the robot’s mass.
Theory
The coefficient of static friction is the fraction of an object’s weight that must be applied to it laterally in order to get it to move. Every combination of two materials has a unique coefficient that must be ascertained experimentally. There are two types of friction: static friction and sliding friction, which is sometimes called kinetic friction. The coefficient of sliding friction is the fraction of an object’s weight that must be applied to it laterally in order to keep it moving after its static friction has been overcome and is usually less than the coefficient of static friction.
Sliding friction should not be applicable to the E-racer, because the surface of the treads should always be stationary with respect to the board as they move the robot. The term coefficient of friction as it appears in the rest of this text refers to the coefficient of static friction. Also, usually the force of friction is caused by gravity, and an outside force needs to be applied perpendicular to gravity in order to overcome the frictional force. In E-racer’s case, the frictional force is caused by the magnetic force, and the force that would oppose the force of friction would be gravity.
In order to use a more general term to avoid confusion, the term normal force is used to refer to the force that is applied orthogonal to the plane of the surfaces which are touching. In this case, the normal force points into the whiteboard. Additionally, the frictional force is the force that opposes the change in motion. Formally, the force of friction is defined as:
Figure 1 – Equation for the force of friction
Where F is the force of friction, ? is the coefficient of friction, and N is the normal force. So the more general definition of the coefficient of friction is the fraction of an object’s normal force that must be applied perpendicular to the normal force in order to get the object to move.
Method
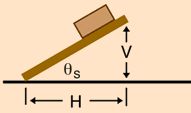
In order to determine a coefficient of friction, an experiment needed to be devised in order to find a relation between the frictional force and the normal force. The secret to devising such an experiment is to use geometry to translate the reading from an instrument into the coefficient. The experiment was conducted by placing a piece of tank tread on a small whiteboard, tilting the board until the tread slipped, and measuring the angle at which it slipped with a leveling application on a smartphone. This angle theta is defined to be the angle between the whiteboard and a level table as shown in Figure 2.
Figure 2 – Visual description of theta
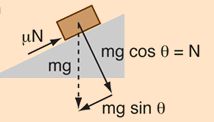
After defining the experiment’s geometry, a free body diagram can be composed to define the forces exerted on the tread. The key to understanding how the free body diagram is useful is to realize that the angle that the board makes with the table is the same angle that the normal force makes with the gravitational force. Using trigonometry it can be shown that the magnitude of the normal force is mgCos(?) where m is the mass of the tread, g is the acceleration of gravity, and ? is the angle that the board makes with the table. Additionally, the frictional force is mgSin(?). These forces can be seen in the free body diagram of Figure 3.
Figure 3 – Free body diagram of the forces
The desired variable, ?, can then be defined in terms of the experiment’s variables. By definition:
Figure 4 – Derivation of the coefficient of friction from the free body diagram
Results
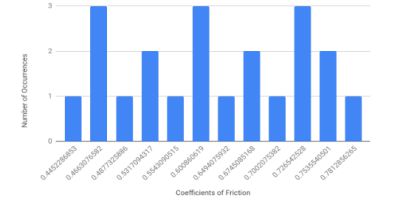
So the coefficient of friction is simply the tangent of the angle between the board and the table. After the methodology of the experiment was established, the experiment was conducted many times to establish an average coefficient of friction. The results of the experiment can be seen below in Figure 5 and 6.
Figure 5 – The tabulated data
Figure 6 – The distribution of 21 tests
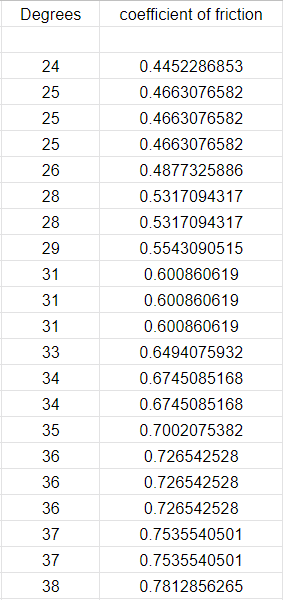
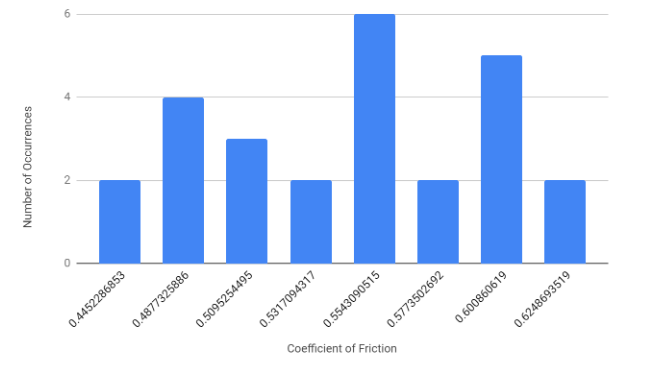
The distribution appears to be trimodal, meaning that three distinct averages seem to be appearing. From this realization, it was concluded that the orientation of the tread was significant. Before the test was conducted, it was assumed that the orientation was insignificant, but the results seemed to deny this assumption. Each orientation: sideways, tread pattern down, and tread pattern up appeared to have their own coefficient. After this new assumption was made, the test was repeated with the tread only its normal operational orientation, tread pattern down. The results of this test can be seen below in Figure 7 and 8. This time the test was conducted 26 times.
Figure 7 – The tabulated data for the second test
Figure 8 – The second round of test with the tread pattern down
The same trimodal distribution occurred, but this time the outer means were less pronounced relative to the inside. The average value was a coefficient of static friction of 0.5449 with a standard deviation of 0.0522.
Conclusion
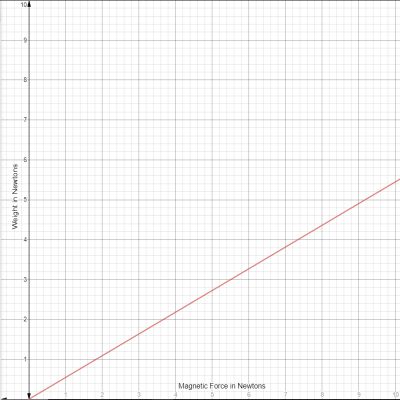
The results of this test confirmed that the frictional force of our robot needs to be about 54.49% of the normal force. In other words, the weight of our robot can’t exceed 54.49% of the attractive force of the magnets, or the robot will lose traction and fall off of the whiteboard. The maximum weight can be plotted as a function of the magnetic force using a simple linear function:
Figure 9 – The coefficient of friction equation applied to our robot
Figure 10 – The maximum weight of the robot as a function of magnetic force