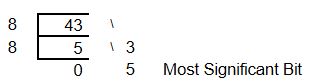Introduction to Arduino Machine Language Programming
READING
The AVR Microcontroller and Embedded Systems using Assembly and C by Muhammad Ali Mazidi, Sarmad Naimi, and Sepehr Naimi
Sections: 0.1, 0.2, 1.1, 2.5, 2.6, 2.7
SOURCE MATERIAL
These are some of the sources I used to develop the material used in the lecture series.
- Reduced Instruction Set Computer
- Atmel AVR Assembler User Guide
- Atmel AVR
- AVR Quick Reference Guide:
- ATmega328P Summary (26 pages)
- ATmega328P (448 pages)
- 8-bit AVR Instruction Set (155 pages)
Table of Contents
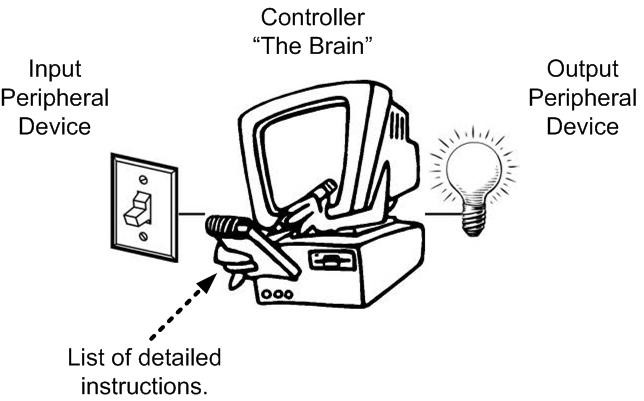
What is an Embedded System?
- An embedded system is an electronic system that contains at least one controlling device, i.e. “the brain”, but in such a way that it is hidden from the end user. That is, the controller is embedded so far in the system that usually users don’t realize its presence.
- Embedded systems perform a dedicated function.
What is the Controlling Device?
| EE Course | Technology | Tools |
| EE201 | Discrete Logic | Boolean Algebra |
| EE301 | Field Programmable Gate Array (FPGA), Application-Specific Integrated Circuit (ASIC) | HDL (typically VHDL or Verilog) |
| EE346 | Microcontroller | Program (typically C++ or Assembly) |
| EE443 | System on a Chip (SoC) | System Level Design Language |
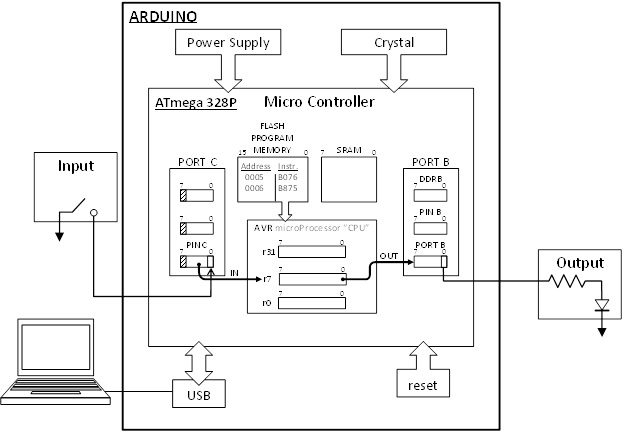
What is an Arduino
- Arduino is an open-source electronics PCB containing a microcontroller and the things needed to support it: Power Supply, Communications, Reset Button, Clock, and Connectors for adding Sensors and Actuators in the physical world.
-
Using an Arduino you can develop interactive objects, taking inputs from a variety of switches or sensors, and controlling a variety of lights, motors, and other physical outputs.
- The Arduino consists of two parts; the hardware and the software.
- We will be using the Arduino Uno which contains an ATmega328P 8 bit microcontroller.
- We will be using AVR Studio to develop the software for the Arduino in place of the Arduino IDE and associated Scripting Language.
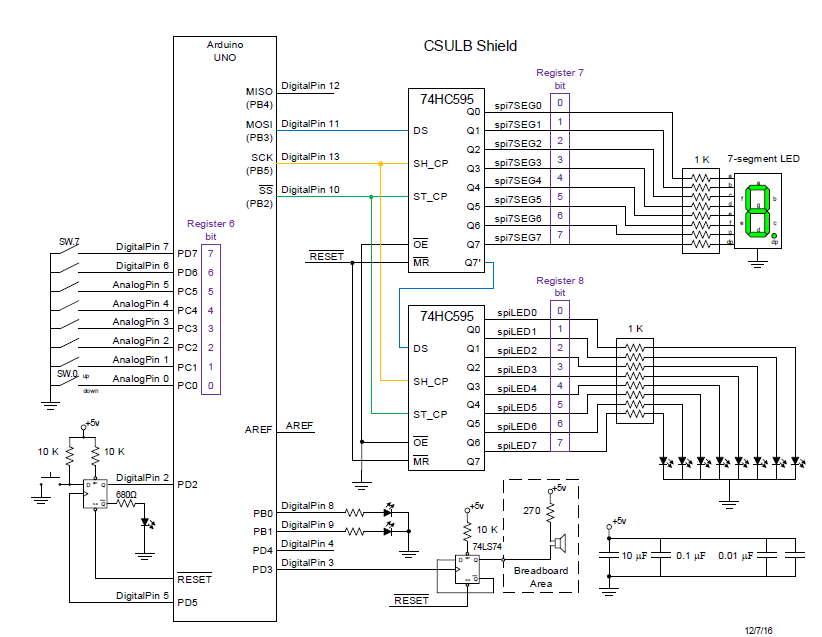
What is a CSULB Shield
- The CSULB Shield was designed to meet the educational objectives of EE 346.
- The shield works with the Arduino Uno, Duemilanove (rev 2009b), and Mega Microcontroller Boards.
- CSULB Shield Specifications
- Input
- 8 Toggle Switches
- General Purpose Push Button
- Reset Button
- Output
- 8 Discrete Red LEDs
- 3 Discrete Green LEDs
- 1 7-Segment Display
- Input
The Building Blocks of an Embedded System
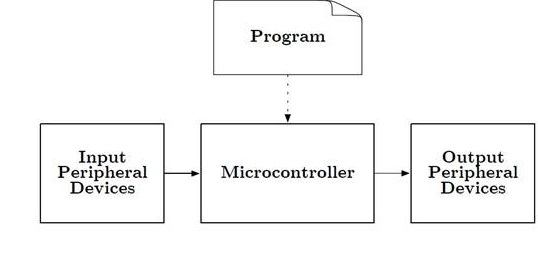
What is an Input and Output Peripheral Device?
- A device attached to a controlling mechanism, for example a computer, yet is not actually part of the controlling mechanism, and whose operation is functionally dependent upon the controlling mechanism.
How do you design this controlling mechanism?
- If you control peripherals using Discrete Electronics or a Programmable Logic Device (PLD) such as an FPGA or ASIC, then the control is in hardware (EE201, EE301).
- If you control peripherals using a Microcontroller then the control is in software (EE346 and EE444), implemented by a Program.
- If you control peripheral using a System on a Chip (SoC) then the control may be in software and/or hardware (EE443).
What is a Program?
- The Program is a “very specific list of instructions” to the computer.
- The process of “creating the program” is where much of an electrical engineer’s time is spent.
- The program is often referred to as Software, while the physical system components are called Hardware. Software held within non-volatile memory is called Firmware.
- Software design is all about creating patterns of 0’s and 1’s in order to get the computer to do what we want. These 0’s and 1’s are known as Machine Code.
0010 0111 0000 0000 → 1110 1111 0001 1111 → 1011 1001 0000 0111 → 1011 1001 0001 1000
1011 1001 0000 0100 → 1011 0000 0111 0110 → 1011 1000 0111 0101 → 1100 1111 1111 1101
- The architecture of the processer (or computer) within a microcontroller is unique as are the Machine Code Instructions it understands.
0010 0111 0000 0000
1110 1111 0001 1111
- The list of Machine Code Instructions understood by a Microcontroller is known as the Machine Language.
How is Machine Code Related to Assembly Language?
Machine Code (The language of the machine)
- Binary Code (bit sequence) that directs the computer to carry out (execute) a pre-defined operation.
0010 0111 0000 0000
1110 1111 0001 1111
1011 1001 0000 0111
1011 1001 0001 1000
Assembly Language
- A computer language where there is a one-to-one correspondence between a symbolic (assembly language instruction) and a machine code
- The language of the machine in human readable form
clr r16
ser r17
out DDRC, r16
out PORTC, r17
Corollary
- Specific to a single computer or class of computers (non-portable)
Anatomy of an Assembly Instruction
Sample Code Segment
| Machine Code | Assembly Code | |
| Binary | Hex | |
| 0010 0111 0000 0000 | 0x2700 | clr r16 |
| 1110 1111 0001 1111 | 0xEF1F | ser r17 |
| 1011 1001 0000 0111 | 0xB907 | out DDRC, r16 |
| 1011 1001 0001 1000 | 0xB918 | out PORTC, r17 |
- The Operation Code or Opcode for short, is a mnemonic that tells the CPU what instruction is to be executed. In the sample code above that would be clr (clear), ser (set register), and out (output to I/O location). One or more operands follow the Opcode.
- The Operand(s) specify the location of the data that is to be operated on by the CPU. In many cases it is the Arithmetic Logic Unit (ALU) that performs the specified operation.
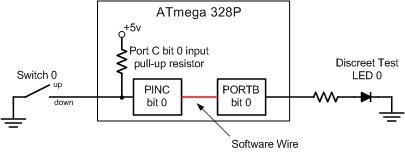
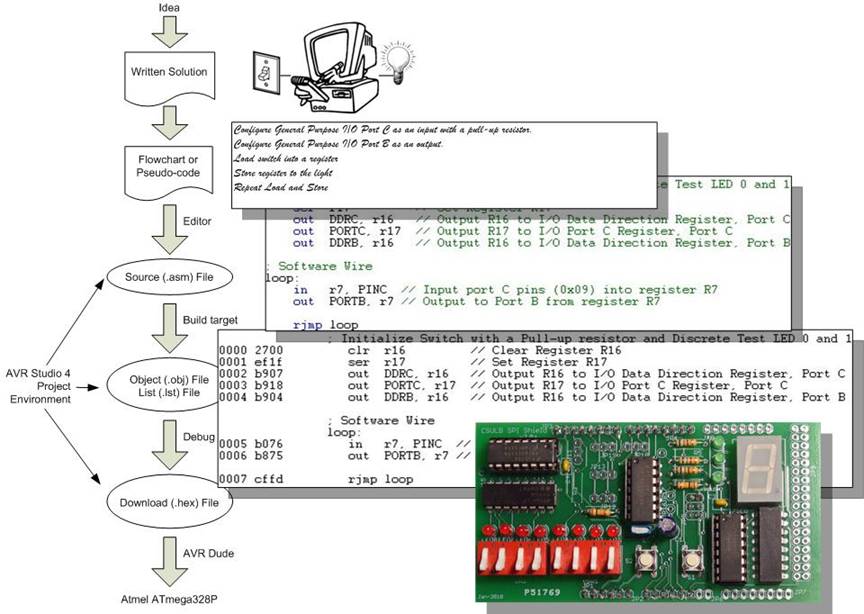
Design Example
Write an Assembly Program to turn a light on and off with a switch. A similar program was used in the design of The Wake-up Machine.
Development Steps
Assembly and Microcontroller Overview
Help
0010 0111 0000 00002 = 270016 = clr r16…
An Important part of this course is understanding the Design and Language of “The Computer.”
The computer implements the classical digital gate you learned in your Digital Logic class (EE201) in software with instructions like and, or, and eor/xor.
You are also going to have to seamlessly move from binary to hexadecimal and back again (i.e., Number Systems).
Computer programs move data through Registers, so a working knowledge of Flip-Flops and Registers is also an important foundational part of this class.
Finally, instead of designing with gates (EE201) you will be designing with code. So you will need to review Programming concepts like: data transfer (assignment expressions) , arithmetic and logic operators, control transfer (branching and looping), and bit and bit test operators that you leaned in your programming class (CECS174 or CECS100).
The good news is that help is available in Chapter 0: “Introduction to Computing” of your textbook, the supplemental reading provided at the beginning of this document, the web, and Appendix A – Number Systems.
Appendix
Numbers and Their Computer Representation
Introduction
Base 10 result of ten fingers
Arabic symbols 0-9, India created Zero and Positional Notation
Other Systems: Roman Numerals: essentially additive, Importance of Roman Numeral lies in whether a symbol precedes or follows another symbol. Ex. IV = 4 versus VI = 6. This was a very clumsy system for arithmetic operations.
Positional Notation (Positive Real Integers)
Fractional numbers will not be considered but it should be noted that the addition of said would be a simple and logical addition to the theory presented.
The value of each digit is determined by its position. Note pronunciation of 256 “Two Hundred and Fifty Six?
Ex. 256 = 2*102 + 5*101 + 6*100
Generalization to any base or radix
Base or Radix = Number of different digit which can occur in each position in the number system.
N = Anrn + An-1rn-1 + … + A1r1 + A0r0 (or simple A1r + A0)
Introduction to Binary System
The operation of most digital devices is binary by nature, either they are on or off.
Examples: Switch, Relay, Tube, Transistor, and Transistor-Transisor-Logic Integrated circuit (TTL IC)
Thus it is only logical for a digital computer to in base 2.
Note: Future devices may not have this characteristic, and this is one of the reasons the basics and theory are important. For they add flexibility to the system.
In the Binary system there are only 2 states allowed; 0 and 1 (FALSE or TRUE, OFF or ON)
Example: Most Significant Bit
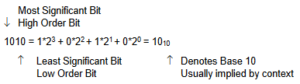 Bit = One Binary Digit (0 or 1)
Bit = One Binary Digit (0 or 1)
This positional related equation also gives us a tool for converting from a given radix to base 10 – in this example Binary to Decimal.
Base Eight and Base Sixteen
Early in the development of the digital computer Von Neuman realized the usefulness of operating in intermediate base systems such as base 8 (or Octal)
By grouping 3 binary digits or bits one octal digit is formed. Note that 23 = 8
Binary to Octal Conversion Table
222120
0 0 0 = 0
0 0 1 = 1
0 1 0 = 2
0 1 1 = 3
1 0 0 = 4
1 0 1 = 5
1 1 0 = 6
1 1 1 = 7 Symbols (not numbers) 8 and 9 are not used in octal.
Example: 100 001 010 110
4 1 2 6 8 = 4*83 + 1*82 + 2*81 + 6*80 = 2134
This is another effective way of going from base 2 to base 10
Summary: Base 8 allows you to work in the language of the computer without dealing with large numbers of ones and zeros. This is made possible through the simplicity of conversion from base 8 to base 2 and back again.
In microcomputers groupings of 4 bits (as opposed to 3 bits) or base 16 (24) is used. Originally pronounced Sexadecimal, base 16 was quickly renamed Hexadecimal (this really should be base 6).
Binary to Hex Conversion Table
23222120
0 0 0 0 = 0
0 0 0 1 = 1
0 0 1 0 = 2
0 0 1 1 = 3
0 1 0 0 = 4
0 1 0 1 = 5
0 1 1 0 = 6
0 1 1 1 = 7
1 0 0 0 = 8
1 0 0 1 = 9
1 0 1 0 = A
1 0 1 1 = B
1 1 0 0 = C
1 1 0 1 = D
1 1 1 0 = E
1 1 1 1 = F
In Hex Symbols for 10 to 15 are borrowed from the alphabet. This shows how relative numbers really are or in other words, they truly are just symbols.
Example: 1000 0101 0110
8 5 6 16 = 8*162 + 5*161 + 6*160 = 2134
It is not as hard to work in base 16 as you might think, although it does take a little practice.
Conversion from Base 10 to a Given Radix (or Base)
Successive Division is best demonstrated by an example
To get the digits in the right order let them fall to the right.
For this example: 4310 = 1010112 Quick Check (Octal) 101 011 = 5*8 + 3 = 4310
Another example: Convert 4310 from decimal to Octal
For this example: 4310 = 538 Quick Check (Octal) 5*8 + 3 = 4310
Generalization of the procedure OR Why It Works
Where r = radix, N = number, A = remainder, and n = the number of digits in radix r for number N. Division is normally done in base 10.
Another way of expressing the above table is:
N = r*N1 + A0
N1 = r*N2 + A1
N2 = r*N3 + A2
:
Nn-1 = r*Nn + An-1
Nn = r*0 + An
or (now for the slight of hand)
N = r*( r*N2 + A1)+ A0 substitute N1
N = r2N2 + rA1+ A0 multiply r through equation
N = r2(r*N3 + A2) + rA1+ A0 substitute N2
:
N = Anrn + An-1rn-1 + … + A1r1 + A0r0
Nomenclature
Bit = 1 binary digit
Byte = 8 bits
Nibble = one half byte = 4 bits
Word = Computer Dependent
Binary Arithmetic
Binary Addition
Binary addition is performed similar to decimal addition using the following binary addition rules:
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 10 (0 with a carry of 1)
Examples:
| Problem | 2110 + 1010 = 3110 | 4510 + 5410 = 9910 | 310 + 710 = 1010 |
| 101012
+ 010102 _______________ 111112 |
1011012
+ 1101102 _______________ 11000112 |
0112
+ 1112 _______________ 10102 |
|
| Check | 1*23 + 0*22 + 1*21 + 0*20 =
1*8 + 0*4 + 1*2 + 0*1 = 1010 |
Octal Addition
Octal addition is also performed similar to decimal addition except that each digit has a range of 0 to 7 instead of 0 to 9.
| Problem | 2110 + 1010 = 3110 | 4510 + 5410 = 9910 | 310 + 710 = 1010 |
| 258
+ 128 _______________ 378 |
558 + 668 _______________ 1438 |
38 + 78 _______________ 128 |
|
| Check | 3*81 + 7*80
3*8 + 7*1 = 3110 |
1*82 + 4*81 + 3*80
64 + 32 + 3 = 9910 |
1*81 + 2*80
8 + 2 = 1010 |
Hexadecimal Addition
Hex addition is also performed similar to decimal addition except that each digit has a range of 0 to 15 instead of 0 to 9.
| Problem | 2110 + 1010 = 3110 | 4510 + 5410 = 9910 | 310 + 710 = 1010 |
|
1516 + 0A16 _______________ 1F16 |
2D16 + 3616 _______________ 6316 |
316 + 716 _______________ A16 (not 10) |
|
| Check | 1*161 + 15*160
16 + 15 = 3110 |
6*161 + 3*160
96 + 3 = 9910 |
10*160
1010 |
Binary Multiplication
| Decimal | Binary |
|
1110 x 1310 _______________ 3310 1110– _______________ 14310 |
10112 x 11012 _______________ 10112 00002- 10112– 10112— _______________ 100011112 |
| Check | 8*161 + 15*160
128 + 15 = 14310 |
Binary Division
Check: 1*161 + 5*160 = 16 + 5 = 2110
Practice arithmetic operations by making problems up and then checking your answers by converting them back to base 10 via different bases (i.e., 2, 8, and 16).
How a computer performs arithmetic operations is a much more involved subject and has not been dealt with in this section.
Complements and Negative Numbers OR Adding a Sign Bit
Addition, Multiplication, and Division is nice but what about subtraction and negative numbers? From grade school you have learned that subtraction is simply the addition of a negative number. Mathematicians along with engineers have exploited this principle along with modulo arithmetic — a natural outgrowth of adders of finite width — to allow computers to operate on negative numbers without adding any new hardware elements to the arithmetic logic unit (ALU).
Sign Magnitude
Here is a simple solution, just add a sign bit. To implement this solution in hardware you will need to create a subtractor; which means more money.
sign magnitude
Example: – 2 = 1 00102
Ones Complement
Here is a solution that is a little more complex. Add the sign bit and invert each bit making up the magnitude — simply change the 1’s to 0’s and the 0’s to 1’s.
sign magnitude
Example: – 2 = 1 11012
To subtract in 1’s complement you simply add the sign and magnitude bits letting the last carry bit (from the sign) fall into the bit bucket, and then add 1 to the answer. Once again let the last carry bit fall into the bit bucket. The bit bucket is possible due to the physical size of the adder.
0 10102 10
+ _ 1 11012 +(-2)
0 10002 8
+______12 Adjustment
0 10012
Although you can now use your hardware adder to subtract numbers, you now need to add 1 to the answer. This again means adding hardware. Compounding this problem, ones complement allows two numbers to equal 0 (schizophrenic zero).
Twos Complement
Here is a solution that is a little more complex to set up, but needs no adjustments at the end of the addition. There are two ways to take the twos complement of a number.
Method 1 = Take the 1’s complement and add 1
__0 00102 2 <- start
+ 1 11012 1’s complement (i.e. invert)
+ 12 add 1
1 11102
Method 2 = Move from right to left until a 1 is encountered then invert.
| 0 00102 | start = 210 |
| 02 | no change |
| 102 | no change but one is encountered |
| 1102 | invert = change 0 to 1 |
| 11102 | invert = change 0 to 1 |
| 1 11102 | invert = change 0 to 1 |
Subtraction in twos complement is the same as addition. No adjustment is needed, and twos complement has no schizophrenic zero although it does have an additional negative number (see How It Works).
0 10102 10
+ 1 11102 +(-2)
0 10012 8
Examples:
| Problem | 3310 – 1910 = 1410 | 6910 – 8410 = -1510 |
|
0 1000012 + 1 1011012 _______________ 0 0011102 |
0 10001012 + 1 01011002 _______________ 1 11100012 |
|
| Check | convert to intermediate base E16 = 1410 | convert back to sign magnitude
– 00011112 convert to intermediate base (16) – F16 = – 1510 |
Why It Works
Real adders have a finite number of bits, which leads naturally to modulo arithmetic — the bit bucket.
Overflow
With arithmetic now reduced to going around in circles, positive numbers can add up to negative and vice-versa. Two tests provide a quick check on whether or not an “Overflow” condition exists.
Test 1 = If the two numbers are negative and the answer is positive, an overflow has occurred.
Test 2 = If the two number are positive and the answer is negative, an overflow has occurred.
If computers were calculators and the world was a perfect place, we would be done. But they are not and so we continue by looking at a few real world problems and their solutions.
Character Codes OR Non-Numeric Information
Decimal Number Problem
Represent a Decimal Numbers in a Binary Computer. A binary representation of a decimal number, a few years ago, might have been “hard wired” into the arithmetic logic unit (ALU) of the computer. Today it, more likely than not, is simply representing some information that is naturally represented in base 10, for example your student ID.
Solution
In this problem, ten different digits need to be represented. Using 4 bits 24 or 16 combinations can be created. Using 3 bits 23 or 8 combinations can be created. Thus 4 bits will be required to represent one Decimal Digit. It should here be pointed out how 16 combinations can be created from 4 bits (0000 – 1111) while the largest numeric value that can be represented is 15. The reason that the highest numeric value and the number of combinations are different, is due to zero (0) being one of the combinations. This difference points up the need to always keep track of wetter or not you are working zero or one relative and what exactly you are after — a binary number or combinations.
The most common way of representing a decimal number is named Binary Coded Decimal (BCD). Here each binary number corresponds to its decimal equivalent, with numbers larger than 9 simply not allowed. BCD is also known as an 8-4-2-1 code since each number represents the respective weights of the binary digits. In contrast the Excess-3 code is an unweighted code used in earlier computers. Its code assignment comes from the corresponding BCD code plus 3. The Excess-3 code had the advantage that by complementing each digit of the binary code representation of a decimal digit (1’s complement), the 9’s complement of that digit would be formed. The following table lists each decimal digit and its BCD and Excess-3 code equivalent representation. I have also included the negative equivalent of each decimal digit encoded using the Excess-3 code. For instance, the complement of 0100 (1 decimal) is 1011, which is 8 decimal. You can find more decimal codes on page 18 of “Digital Design” by M. Morris Mano (course text).
| Binary Coded Decimal (BCD) | Excess-3 | |||
| Decimal Digit | Binary Code 8‑4-2-1 | Decimal Digit | Binary Code | 9’s Compliment |
|
0 1 2 3 4 5 6 7 8 9 N/A N/A N/A N/A N/A N/A |
0000
0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 |
N/A
N/A N/A 0 1 2 3 4 5 6 7 8 9 N/A N/A N/A |
0000
0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 |
1111 1110 1101 1100 1011 1010 1001 1000 0111 0110 0101 0100 0011 0010 0001 0000 |
Alphanumeric Character Problem
Represent Alphanumeric data (lower and upper case letters of the alphabet (a-z, A-Z), digital numbers (0-9), and special symbols (carriage return, line feed, period, etc.).
Solution
To represent the upper and lower case letters of the alphabet, plus ten numbers, you need at least 62 (2×26+10) unique combinations. Although a code using only six binary digits providing 26 or 64 unique combinations would work, only 2 combinations would be left for special symbols. On the other hand a code using 7 bits provides 27 or 128 combinations, which provides more than enough room for the alphabet, numbers, and special symbols. So who decides which binary combinations correspond to what character. Here there is no “best way.” About thirty years ago IBM came out with a new series of computers which used 8 bits to store one character (28 = 256 combinations), and devised the Extended Binary-Coded Decimal Interchange Code (EBCDIC pronounced ep-su-dec) for this purpose. Since IBM had a near monopoly on the computer field, at that time, the other computer makers refused to adopt EBCDIC, and that is how the 7bit American Standard Code for Information Interchange (ASCII) came into existence. ASCII has now been adopted by virtually all micro-computer and mini-computer manufacturers. The table below shows a partial list of the ASCII code. Page 23 of the text lists all 128 codes with explanations of the control characters.
| DEC | HEX | CHAR | DEC | HEX | CHAR |
| 32
33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 |
20
21 22 23 24 25 26 27 28 29 2A 2B 2C 2D 2E 2F 30 31 32 33 34 35 36 37 38 39 3A 3B 3C 3D 3E 3F |
!
“ # $ % & ‘ ( ) * + , – * / 0 1 2 3 4 5 6 7 8 9 : ; < = > ? |
64
65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 |
40
41 42 43 44 45 46 47 48 49 4A 4B 4C 4D 4E 4F 50 51 52 53 54 55 56 57 58 59 5A 5B 5C 5D 5E 5F |
@
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z [ ] ^ _ |
The word “string” is commonly used to describe a sequence of characters stored via their numeric codes — like ASCII).
Although ASCII requires only 7 bits, the standard in computers is to use 8 bits, where the leftmost bit is set to 0. This allows you to code another 128 characters (including such things as Greek letters), giving you an extended character set, simply by letting the leftmost bit be a 1. This can also lead to a computer version of the tower of Babel. Alternatively, the leftmost bit can be used for detecting errors when transmitting characters over a telephone line. Which brings us to our next problem.
Synthesis
Although ASCII solves the communication problem between English speaking computers, what about Japanese, Chinese, or Russian computers which have different, and in all these examples, larger alphabets?
Communication Problem
Binary information may be transmitted serially (one bit at a time) through some form of communication medium such as a telephone line or a radio wave. Any external noise introduced into the medium can change bit values from 1 to 0 or visa versa.
Solution
The simplest and most common solution to the communication problem involves adding a parity bit to the information being sent. The function of the parity bit is to make the total number of 1’s being sent either odd (odd parity) or even (even parity). Thus, if any odd number of 1’s were sent but an even number of 1’s received, you know an error has occurred. The table below illustrates the appropriate parity bit (odd and even) that would be appended to a 4-bit chunk of data.
Synthesis
What happens if two binary digits change bit values? Can a system be devised to not only detect errors but to identify and correct the bit(s) that have changed? One of the most common error-correcting codes was developed by R.W. Hamming. His solution, known as a Hamming code, can be found in a very diverse set of places from a Random Access Memory (RAM) circuit to a Spacecraft telecommunications link. For more of error correcting codes read pages 299 to 302 of the text.
Although detecting errors is nice, preventing them from occurring is even better. Which of course brings us to our next problem.
Shaft Encoder Problem
As a shaft turns, you need to convert its radial position into a binary coded digital number.
Solution
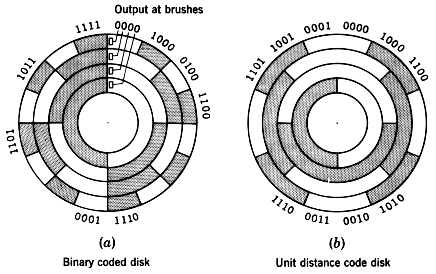
The type of coder which will be briefly described below converts a shaft position to a binary-coded digital number. A number of different types of devices will perform this conversion; the type described is representative of the devices now in use, and it should be realized that more complicated coders may yield additional accuracy. Also, it is generally possible to convert a physical position into an electric analog-type signal and then convert this signal to a digital system. In general, though, more direct and accurate coders can be constructed by eliminating the intermediate step of converting a physical position to an analog electric signal. The Figure below illustrates a coded-segment disk which is coupled to the shaft.
The shaft encoder can be physically realized using electro-mechanical (brush) or electro-optical technology. Assuming an electro-optical solution, the coder disk is constructed with bands divided into transparent segments (the shaded areas) and opaque segments (the unshaded areas). A light source is put on one side of the disk, and a set of four photoelectric cells on the other side, arranged so that one cell is behind each band of the coder disk. If a transparent segment is between the light source and a light-sensitive cell, a 1 output will result; and if an opaque area is in front of the photoelectric cell, there will be a O output.
There is one basic difficulty with the coder illustrated: if the disk is in a position where the output number is changing from 011 to 100, or in any position where several bits are changing value, the output signal may become ambiguous. As with any physically realized device, no matter how carefully it is made, the coder will have erroneous outputs in several positions. If this occurs when 011 is changing to 100, several errors are possible; the value may be read as 111 or 000, either of which is a value with considerable errors. To circumvent this difficulty, engineers use a “Gray,” or “unit distance,” code to form the coder disk (see previous Figure). In this code, 2 bits never change value in successive coded binary numbers. Using a Gray coded disk, a 6 may be read as 7, or a 4 as 5, but larger errors will not be made. The Table below shows a listing of a 4-bit Gray code.
| Decimal | Gray Code |
|
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
0000
0001 0011 0010 0110 0111 0101 0100 1100 1101 1111 1110 1010 1011 1001 1000 |
Synthesis
Gray code is used in a multitude of application other than shaft encoders. For example, CMOS circuits draw the most current when they are switching. If a large number of circuits switch at the same time unwelcome phenomena such as “Ground Bounce” and “EMI Noise” can result. If the transistors are switching due to some sequential phenomena (like counting), then these unwelcome visitors can be minimized by replacing a weighted binary code by a Gray code.
If the inputs to a binary machine are from an encoder using a Gray code, each word must be converted to conventional binary or binary-coded decimal bit equivalent. How can this be done? Before you can answer this question, you will need to learn about Boolean Algebra — what a coincidence, that’s the topic of the next Section.
ATmega328P Instruction Set (Page 12-14)